Previous instalments
General Data Structures
Trees
If you haven’t read my previous post on General Trees, it might be a good idea to do so before reading further.
A Binary Tree is a refined version of the General Tree that limits the number of children each node can have - two to be exact. Child nodes are thus referred to as the Left and Right child nodes. The BinaryTree<T> class in NGenerics provides an implementation of a Binary Tree, which, when simplified, looks something like this :
public class BinaryTree
{
BinaryTree Left { get; set; }
BinaryTree Right { get; set; }
T Data { get; set; }
}
We can represent a simple binary tree visually like this:
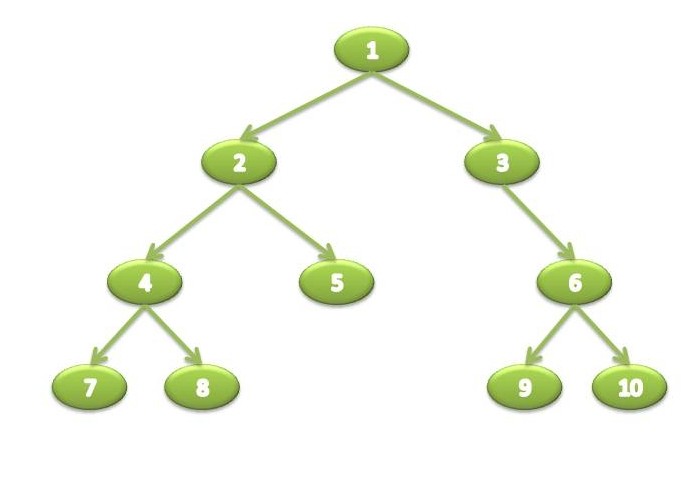
Binary Trees support pre-order and post-order traversal as discussed in my previous post, and also support in-order traversal. An in-order traversal visits the left node, the root node and lastly the node on the right. When supplied with an InOrderVisitor instance, the visitor will visit tree nodes in the order (7, 4, 8, 2, 5, 1, 3, 9, 6, 10) :
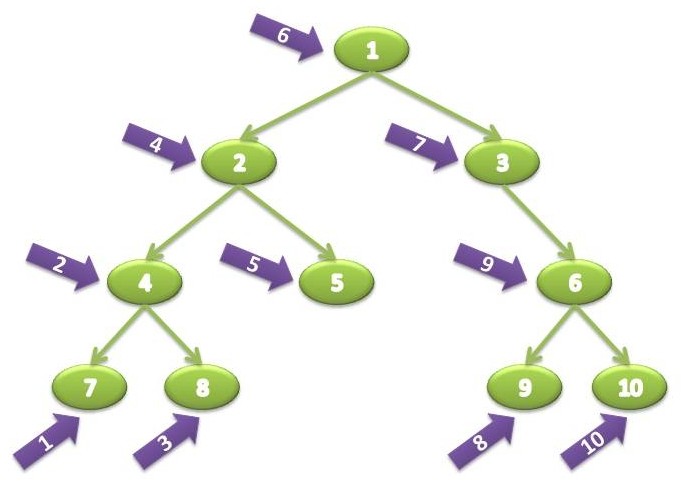
As with General Trees, the BinaryTree<T> class supports breadth first traversal and has ICollection<T> semantics.
Binary Search Trees
Search trees attempt to address the problem of reducing the number of comparisons in finding items. While not as efficient as Hash tables with their O(1) performance, they do cut down search times over larger data sets. Search trees are able to do this by adding constraints to tree data structures. A Binary Search Tree is the simplest of search trees with the following rules in place:
- Each value in the tree is distinct from any other (unique).
- Each left child node has a value smaller than the value of its parent.
- Each right child node has a value larger than the value of its parent.
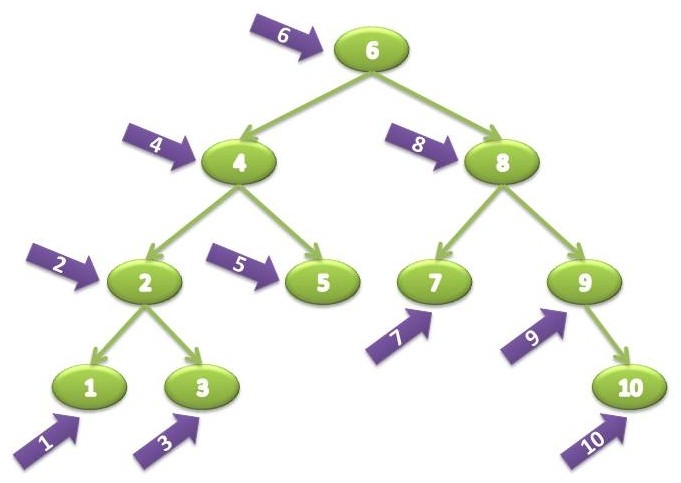
The BinarySearchTree<TKey, TValue> class in NGenerics implements the IDictionary<TKey, TValue> interface for simple lookups based on keys, and supports the usual traversal algorithms. Re-using our example tree and changing it to comply to the rules could result in the following tree:
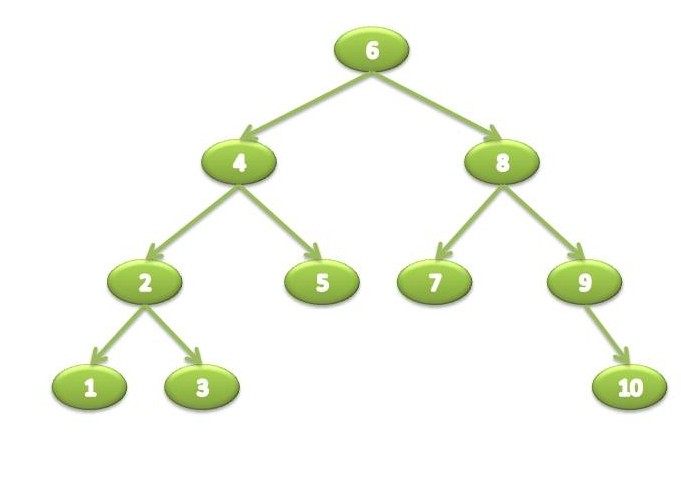
It’s easy to see how a Binary Tree can cut down search times - when using a sequential data structure (array, list), or when manually searching an unordered tree like the plain BinaryTree, we potentially need to search through every item in the collection before we find it with a worst-case performance of O(n). With Binary Search Trees we can cut down that time by comparing node values with the search value and deciding on which branch to continue searching on - enough to make searching a Binary Trees on average an O(log n) operation. To illustrate, searching for the value “3” in our sample tree will result in 4 comparisons :
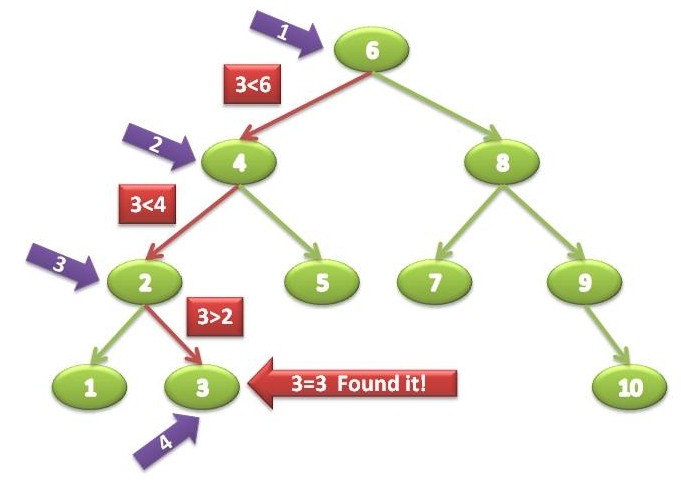
Although Binary Trees are not nearly as efficient as hash tables with regards to searching (assuming that you’ve implemented a proper hash function), Binary Search Trees (and most other search trees) provide an enormous benefit over hash tables in that we can traverse items in sorted order without any preprocessing. We can use an in-order traversal to yield items in sorted order:
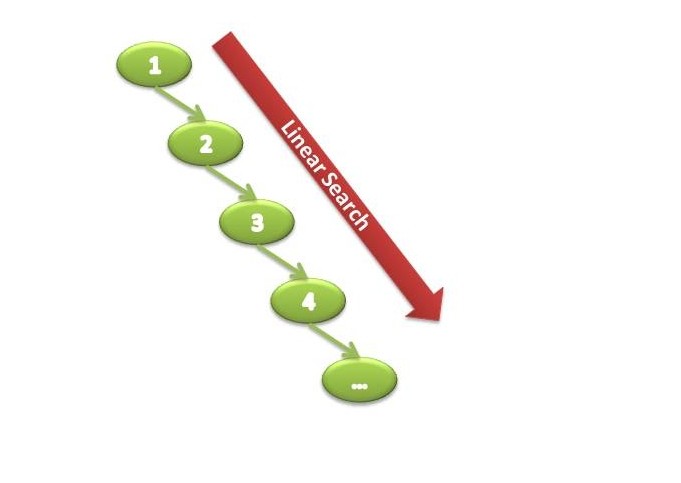
Binary Trees do suffer from a couple of worst-case performance scenarios where there performance could degrade to O(n) in searches. Adding items to the tree in ascending order will result in the following worst-case scenario:
Adding items in descending order will result in a tree that grows in the opposite direction, with the same devastating effect. Self-balancing trees address this problem but that’s a topic for a future post. If the data you’re pumping into the tree is random you’ll probably never hit this situation - but if you have data with some order in it a self-balancing tree might be a better fit.
Photo by Andrew Haimerl on Unsplash